2 Básico do básico do R e RStudio

2.1 Os paineis

Ao abrir o RStudio você encontrará os seguintes paineis (Figura 2.1).

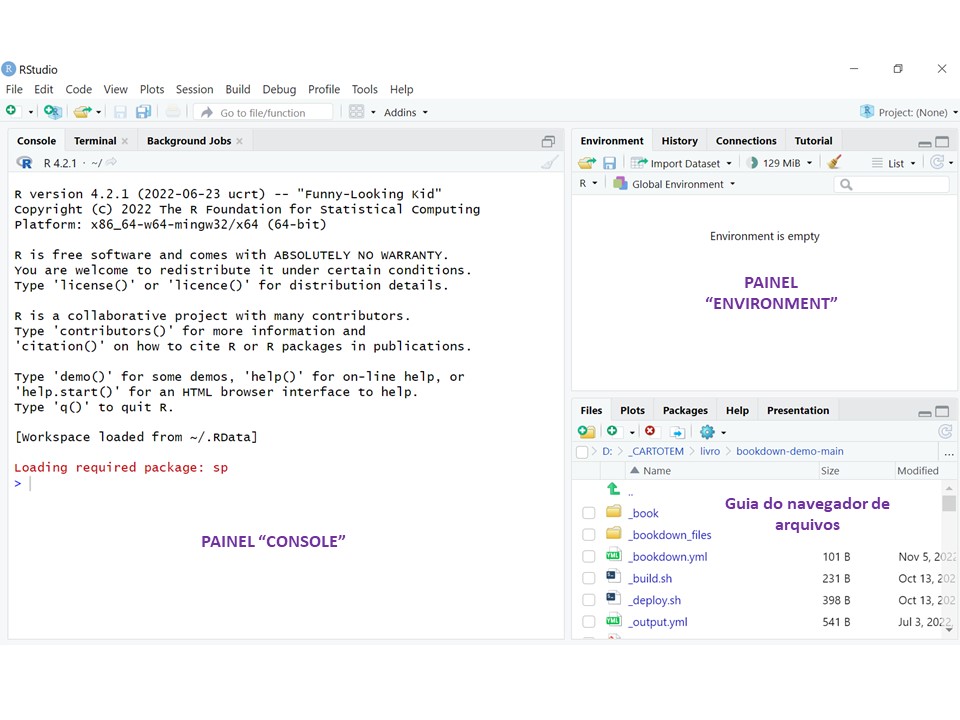
Figure 2.1: Tela do RStudio

O painel “console” é o R propriamente dito; onde você pode digitar os comandos e executá-los diretamente. As outras janelas são opcionais existentes no RStudio para facilitar as tarefas. É recomendado utilizar o painel de Editor de Texto (ou script) pois você pode digitar comentários sobre os comandos para que possa se recordar futuramente ou para que outra pessoa possa compreender o raciocínio percorrido. Para abrir um script, use o menu File/New file/R script. Desta forma, terá uma tela como a da Figura 2.2.

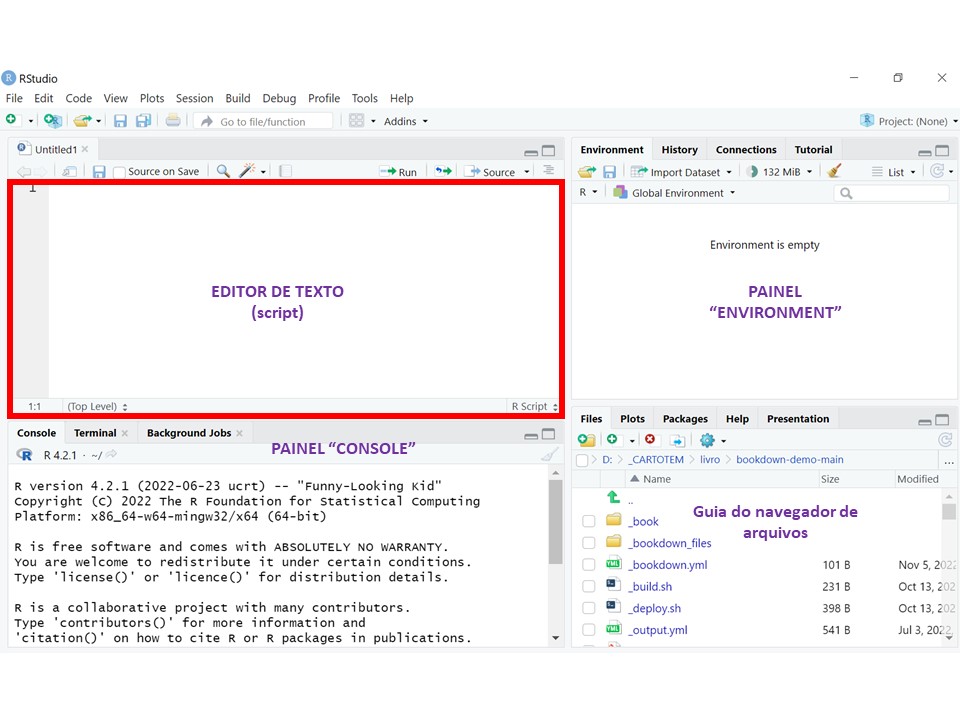
Figure 2.2: Tela do script

O script permite a digitação de um texto sem formatação, como no Bloco de Notas do Windows. No lado direito, encontramos o painel “Environment” (ou Ambiente, em português) onde são listados os objetos e funções da sessão corrente. No lado inferior direito existe o navegador de arquivos entre outras guias que serão vistas no decorrer das atividades. O navegador de arquivos funciona como o “Explorer” do Windows, onde você pode apagar, renomear e gerenciar os arquivos.

O script do RStudio apresenta algumas funcionalidades muito úteis, tais como a conclusão do código. Ao digitar parte de um código, opções de códigos semelhantes surgirão e poderão ser completados ao se utilizar a tecla Tab. Além deste, o RStudio também armazena a história dos comandos. Assim, usando as teclas com as setas para cima ou para baixo, você pode navegar nos comandos anteriores.

O R é um programa de linha de comando, ou seja, após abri-lo, digitamos o código no script. Para executá-lo, você pode selecionar a linha digitada e as teclas Ctrl+Enter para enviar a linha para o seu interpretador. Ou pode usar o comando Run que fica na barra de cima do script. Todos os códigos do R são baseados em inglês e seus nomes, normalmente, dão dicas a respeito do seu uso.

O símbolo > no início da última linha exibida no console chama-se prompt e indica que o R está pronto para receber comandos. Todos as funções terminam com (). Quando quiser fechar o R, utilize a função quit(). O programa lhe perguntará se quer salvar a área de trabalho. Escolha “Yes” se quiser continuar o trabalho da próxima vez que abrir o R na mesma pasta. Os objetos criados serão salvos no arquivo .RData e o histórico de todos os comandos digitados no arquivo .Rhistory. Se quiser sair sem salvar a área de trabalho e o histórico, escolha “No”. O comando quit() possui uma versão mais curta q().

A acentuação no R pode ficar com caracteres estranhos devido à incompatibilidade com a língua portuguesa. Para resolver este problema, vamos ajustar para português.

#para ajustar a língua para portugues usando a função
Sys.setlocale(category = "LC_ALL", locale = "pt_BR.UTF-8")

## [1] "LC_COLLATE=pt_BR.UTF-8;LC_CTYPE=pt_BR.UTF-8;LC_MONETARY=pt_BR.UTF-8;LC_NUMERIC=C;LC_TIME=pt_BR.UTF-8"

Neste livro, os comandos a serem digitados no script do R estão coloridos de forma a facilitar a sua interpretação. Os resultados dos comandos impressos no console do R são exibidos aqui precedidos do símbolo ## e de [1] (indica o primeiro elemento requerido). Por exemplo, ao digitar no script do R a primeira linha, a segunda será exibida no console:

"Olá geógraf@s"

## [1] "Olá geógraf@s"

Observe que ao digitar ou colar comandos longos no console, ocupando mais de uma linha, o R adiciona o símbolo + à primeira coluna da tela para indicar que a linha é a continuação do comando anterior.

Crie o hábito de adicionar comentários aos fragmentos de códigos que você digita no script. Para isso, utilize o símbolo # ao começar o comentário. O RStudio ignora tudo o que vier depois deste símbolo. Fazer comentários no código ajuda muito o aprendizado e a recuperar o raciocínio utilizado.

A utilização da função help auxilia enormemente a compreensão das funções. Use ? nome_da_função ou help(nome_da_função). Quando se deparar com algo que não consegue resolver, busque a solução na internet, nos fóruns de discussão sobre o R. Existem páginas como https://stackoverflow.com/, onde os usuários se ajudam mutuamente para a solução de problemas. Existe um grupo com discussão em português https://pt.stackoverflow.com/questions.

2.2 Tipos de objetos

Uma referência bastante interessante para a estruturação deste capítulo é o DataCamp, a primeira plataforma de aprendizado on-line para Ciência de Dados. Os cursos são ministrados em inglês e fornecem a base necessária para a compreensão dos tipos de objetos e manipulação de dados (DataCamp, 2023).

A forma mais simples de utilização do R é como uma calculadora. Vamos fazer um teste: digite na área do script 3 + 4. Selecione esta linha digitada e rode (pressione a tecla Ctrl ao mesmo tempo em que digita a tecla Enter).

3 + 4

## [1] 7

No console, você verá a resposta [1] 7, ou seja, o R retornou um valor [1] solicitado cuja resposta é 7. Observe o painel do “Ambiente”, do lado direito superior. Ele está vazio, ou seja, não atribui a resposta (7) a nenhum objeto. No entanto, se quisermos gravar esta resposta, podemos atribui-la a um objeto, como x ou qualquer outro nome. Uma variável permite que você salve um valor (e.g., 102) ou um objeto (e.g., descrição de uma função, listas, matrizes) em R. Em outro momento, você pode usar o nome da variável armazenada para acessar o valor ou o objeto que foi salvo dentro desta variável. A atribuição a uma variável é feita com os símbolos <-. Este símbolo parece uma flecha apontando para o nome que se quer dar à variàvel e pode ser usado para o outro lado ->.

Rode novamente, agora digitando x seguido dos sinais de menor e de subtração antes da soma desejada. Use espaços antes e depois dos operadores de atribuição <-, mas não entre < e -. O atalho muito útil para <- é pressionar simultaneamente as teclas alt e a tecla menos (Alt + -).

x <- 3 + 4 #dê o nome de "x" ao valor resultante de 3 + 4
3 + 4 -> x #dê ao valor resultante de 3 + 4 o nome de "x"

Observe que agora existe um objeto no painel “Ambiente”. O objeto é x e seu valor é 7. Deve-se observar que para nomear um objeto, o nome deve iniciar com uma letra (A-Z ou a-z) e pode incluir letras, dígitos (0-9), ponto (.) e sublinhado (_). No entanto, os nomes não podem começar com um número ou por um ponto seguido de um número. As palavras “if” e “for” não são permitidas para um objeto. O R discrimina letras maiúsculas de minúsculas nos nomes dos objetos. Assim, Y e y são dois objetos diferentes.

Digite a função typeofpara verificar o tipo de objeto criado.

typeof(x)

## [1] "double"

No caso, o objeto obtido foi do tipo “double”. Se você atribuir a x um outro valor, digamos 8, o valor anterior é apagado e passa a ter o novo valor. Esta modificação afeta apenas os objetos na memória ativa, não os dados que estão no disco rígido (Paradis, 2005). Para excluir um objeto, usa-se a função rm. Por exemplo, rm(x) exclui o objeto x. O comando rm(list=ls()) apaga todos os objetos da memória.

Todos os objetos têm dois atributos intrínsecos: modo (mode) e comprimento (length).

No R, os tipos de dados que são inseridos nos objetos são divididos em:

numeric: armazena números no formato “integer” (inteiro) ou “double” (reais);
character: armazena dados categóricos ou qualitativos por meio de caracteres (variáveis de texto);
logical: armazena variáveis que assumem os valores “FALSE” (falso) ou “TRUE” (verdadeiro). Variáveis lógicas são conhecidas como “booleanas” porque é um tipo de dado lógico que pode ter apenas um de dois valores possíveis: verdadeiro ou falso;
complex: relacionados ao número imaginário “i”.

Quando um número aparece entre aspas (simples ou dupla), o objeto é atribuído a um tipo “character”. Vejamos alguns exemplos:

typeof('20')

## [1] "character"

typeof("20")

## [1] "character"

typeof(20)

## [1] "double"

typeof(FALSE)

## [1] "logical"

typeof(150.4)

## [1] "double"

Para que um número inteiro seja armazenado como “integer” é preciso que seja seguido da letra L. Já vimos que o tipo de objeto x é “double”. Vamos criar um objeto y do tipo “integer”.

y <- 3L + 4L
typeof(y)

## [1] "integer"

Perceba que a classde x é “numeric” e a de y é “integer”. As outras classes são “character” e “logical”.

class(x)

## [1] "numeric"

class(y)

## [1] "integer"

class('20')

## [1] "character"

class(TRUE)

## [1] "logical"

A classe é uma propriedade de um objeto que determina o comportamento das funções aplicadas a ele.

A tabela sistematizada por Aquino (2014), apresenta os operadores matemáticos e lógicos que podemos usar no R e seus significados.

Operador matemático	Significado	Operador lógico	Significado
+	soma	>	maior que
-	subtração	<	menor que
/	divisão	>=	maior ou igual a
*	multiplicação	<=	menor ou igual a
^	exponenciação	&	e
		\|	ou
		==	igual a
		!	não
		!=	diferente de

Quando temos objetos, podemos fazer operações matemáticas entre eles. Por exemplo, vamos criar o objeto laranjas e atribuir o valor de 36. Criamos também o objeto bananas e atribuímos o valor de 48. Agora, podemos ter um novo objeto minhas_frutas, resultante da soma entre bananas e laranjas.

#para criar o objeto 'laranjas'
laranjas <- 36
#para criar o objeto 'bananas'
bananas <- 48
#para criar o objeto 'minhas_frutas'
minhas_frutas <- laranjas + bananas
#para mostrar o objeto 'minhas_frutas'
minhas_frutas

## [1] 84

2.3 Estrutura dos dados

Segundo Wickham (2019), a estrutura dos dados no R pode ser organizada segundo sua dimensionalidade (1 dimensão, 2 dimensões ou n dimensões) e se ela é homogênea (todos os conteúdos são do mesmo tipo) ou heterogênea (conteúdos podem ser de tipos diferentes). A tabela organizada por Wickham (2019), a seguir, mostra os cinco tipos de dados mais frequentemente utilizados em análise de dados.

Dimensão	Homogênea	Heterogênea
1d	Atomic vector	List
2d	Matrix	Data frame
nd	Array

Para saber a estrutura de um objeto, use str(). A função str mostra o modo e o comprimento (número de elementos do objeto). Dados faltantes são representados por NA (not available, ou não disponível, em português). Valores não numéricos são representados por NaN (not a number, ou não é um número, em português).

str(x)

##  num 7

str(y)

##  int 7

2.4 Vetores

Os vetores são matrizes de uma dimensão que podem conter dados numéricos, dados de caracteres ou dados lógicos. Em outras palavras, um vetor é uma ferramenta simples para armazenar dados de um único tipo.

Em R, criamos um vetor com a função c(). Para facilitar a memorização, “c” vem de “concatenate” (concatenar, unir). Os elementos são colocados dentro dos parênteses, separados por vírgula. A partir de vetores é possível fazer cálculos.

Por exemplo, podemos criar vetores para armazenar os dados de temperatura do ar e precipitação média mensal de Mirante do Parnaíba, em São Paulo (Fonte: https://pt.wikipedia.org/wiki/Clima_da_cidade_de_São_Paulo#).

Vamos criar vetores de temperatura média anual do ar, que receberá o nome de temp. Os dados de temp são: 23.1, 23.5, 22.5, 21.2, 18.4, 17.5, 17.2, 18.1, 19.1, 20.5, 21.2, 22.6 (Dica: para ter o exato conjunto de dados, copie e cole desde o primeiro valor até o último dentro dos parênteses da função).

#para criar o objeto 'temp'
temp <- c(23.1, 23.5, 22.5, 21.2, 18.4, 17.5, 17.2, 18.1, 19.1, 20.5, 21.2, 22.6)
#para visualizar 'temp'
temp

##  [1] 23.1 23.5 22.5 21.2 18.4 17.5 17.2 18.1 19.1 20.5 21.2 22.6

A precipitação média anual receberá o nome de prec. Os dados de precipitação arredondados são: 292, 257, 229, 87, 66, 59, 48, 32, 83, 127, 143, 231

#para criar o objeto 'prec'
prec <- c(292, 257, 229, 87, 66, 59, 48, 32, 83, 127, 143, 231)
#para visualizar 'prec'
prec

##  [1] 292 257 229  87  66  59  48  32  83 127 143 231

2.5 Nomeando os vetores

Vimos que podemos criar conjuntos de dados usando a função c() em R. Como temos dados de precipitação e temperatura, seria interessante que estes valores fossem associados ao mês correspondente. Esta tarefa pode ser executada por meio da função names().

Podemos dar os nomes dos meses aos dados de temperatura e precipitação criando um vetor de meses. Atribua a uma variável chamada ‘meses’ o conjunto de nomes dos meses do ano. Os nomes dos meses serão abreviados: “jan”, “fev”, “mar”, “abr”, “mai”, “jun”, “jul”, “ago”, “set”, “out”, “nov”, “dez”. Lembre-se que nomes são textos e, portanto, devem entrar entre aspas.

#para atribuir os meses do ano ao objeto 'meses'
meses <- c("jan", "fev", "mar", "abr", "mai", "jun", "jul", "ago", "set", "out", "nov", "dez")

Agora, atribua o vetor de “meses” diretamente à variável temp usando a função names().

names(temp) <- c(meses) #para atribuir os meses a 'temp'
temp #para imprimir 'temp'

##  jan  fev  mar  abr  mai  jun  jul  ago  set  out  nov  dez 
## 23.1 23.5 22.5 21.2 18.4 17.5 17.2 18.1 19.1 20.5 21.2 22.6

Faça o mesmo para a variável prec.

names(prec) <- c(meses) #para atribuir os meses a 'prec'
prec #para imprimir 'prec'

## jan fev mar abr mai jun jul ago set out nov dez 
## 292 257 229  87  66  59  48  32  83 127 143 231

2.6 Seleção em vetores

Como geógrafos, gostaríamos de saber quanto chove em cada estação do ano. Para chegarmos nesta resposta, começaremos criando variáveis para cada estação do ano com os valores de precipitação correspondentes. Considere primavera contendo os seguintes meses: setembro, outubro e novembro; verão contendo dezembro, janeiro e fevereiro; outono contendo março, abril e maio e, inverno contendo junho, julho e agosto.

Para selecionar elementos de um vetor (e depois em matrizes, dataframes, …), são usados os colchetes []. Dentro dos colchetes são indicados os elementos do conjunto de dados que serão selecionados. Por exemplo, para selecionar a precipitação do mês de janeiro usa-se a seguinte forma de seleção prec[1]. A seleção do segundo elemento seria prec[2] e assim por diante. Em R, o primeiro elemento de um vetor tem a posição 1 (em Python, a primeira posição tem o índice 0). Para selecionar múltiplos elementos de um vetor, são usados os [] contendo o vetor com a posição dos elementos desejados. Como exemplo, se quisermos selecionar as precipitações dos meses de janeiro e dezembro, usamos c(1, 12) entre colchetes, depois de definir o nome da variável que contém os dados.

#para selecionar as precipitações de janeiro e dezembro
prec_selecao <- prec[c(1, 12)]
#para imprimir a seleção
prec_selecao

## jan dez 
## 292 231

Observe que para selecionar intervalos de dados, pode-se usar :. Por exemplo, para criar uma variável selecionando as precipitações durante os meses do primeiro semestre:

#para selecionar as precipitações do semestre 1
prec_semestre1 <- prec[c(1:6)]
#para imprimir prec_semestre1
prec_semestre1

## jan fev mar abr mai jun 
## 292 257 229  87  66  59

Crie os arquivos de precipitação para cada estação do ano: primavera_prec, verao_prec, outono_prec e inverno_prec usando seleção múltipla.

#para criar a 'primavera_prec' a partir de seleção
primavera_prec <- prec[c(9, 10, 11)]
#para criar a 'verao_prec' a partir de seleção
verao_prec <- prec[c(12, 1, 2)]
#para criar a 'outono_prec' a partir de seleção
outono_prec <- prec[c(3, 4, 5)]
#para criar a 'inverno_prec' a partir de seleção
inverno_prec <- prec[c(6, 7, 8)]
#para visualizar os resultados
primavera_prec

## set out nov 
##  83 127 143

verao_prec

## dez jan fev 
## 231 292 257

outono_prec

## mar abr mai 
## 229  87  66

inverno_prec

## jun jul ago 
##  59  48  32

Vamos fazer a seleção segundo estação do ano para a variável ‘temp’.

#para criar a 'primavera_temp' a partir de seleção
primavera_temp <- temp[c(9, 10, 11)]
#para criar a 'verao_temp' a partir de seleção
verao_temp <- temp[c(12, 1, 2)]
#para criar a 'outono_temp' a partir de seleção
outono_temp <- temp[c(3, 4, 5)]
#para criar a 'inverno_temp' a partir de seleção
inverno_temp <- temp[c(6, 7, 8)]
#para visualizar os resultados
primavera_temp

##  set  out  nov 
## 19.1 20.5 21.2

verao_temp

##  dez  jan  fev 
## 22.6 23.1 23.5

outono_temp

##  mar  abr  mai 
## 22.5 21.2 18.4

inverno_temp

##  jun  jul  ago 
## 17.5 17.2 18.1

R permite fazer seleções a partir de operadores lógicos:

< para menor do que
> para maior do que
<= para menor ou igual a
>= para maior ou igual a
== para igual a
!= para não igual a

Suponha que gostaríamos de saber em quais meses do ano temos precipitação acima de 100 mm. Você consegue imaginar como seria a linha de comando? Crie uma variável chamada prec100.

#para selecionar os meses com valores acima de 100 mm de precipitação
prec100 <- prec > 100
#para visualizar os meses que atendem à seleção
prec100

##   jan   fev   mar   abr   mai   jun   jul   ago   set   out   nov   dez 
##  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE

Como você observou, o código criado gerou um resultado lógico mostrando TRUE para meses com valores acima de 100 mm e FALSE para meses com valores abaixo ou até 100 mm. No entanto, gostaríamos de saber também não apenas os meses com precipitação acima de 100 mm, mas também quanto choveu nestes meses. Você pode criar uma nova variável meses_prec100 selecionando diretamente [prec > 100] após prec.

meses_prec100 <- prec[prec > 100]
meses_prec100

## jan fev mar out nov dez 
## 292 257 229 127 143 231

2.7 Totais e médias em vetores

Como queremos compreender um pouco mais as variáveis meteorológicas de São Paulo, precisamos saber os totais de precipitação durante cada estação do ano. Como já temos os valores para cada estação, podemos simplesmente criar novas variáveis (primavera_prec_total, verao_prec_total, outono_prec_total e inverno_prec_total) usando a função de soma, sum(primavera_prec) e assim por diante.

#para criar o total da precipitação na primavera
primavera_prec_total <- sum(primavera_prec)
#para criar o total da precipitação no verão
verao_prec_total <- sum(verao_prec)
#para criar o total da precipitação no outono
outono_prec_total <- sum(outono_prec)
#para criar o total da precipitação no inverno
inverno_prec_total <- sum(inverno_prec)
#para visualizar os totais
primavera_prec_total

## [1] 353

verao_prec_total

## [1] 780

outono_prec_total

## [1] 382

inverno_prec_total

## [1] 139

Sabendo que a função para o cálculo das médias de temperatura é mean(), como você faria para calcular as médias de temperaturas segundo estação do ano?

#para criar a média da temperatura na primavera
primavera_temp_media <- mean(primavera_temp)
#para criar a média da temperatura no verão
verao_temp_media <- mean(verao_temp)
#para criar a média da temperatura no outono
outono_temp_media <- mean(outono_temp)
#para criar a média da temperatura no inverno
inverno_temp_media <- mean(inverno_temp)
#para visualizar as médias
primavera_temp_media

## [1] 20.26667

verao_temp_media

## [1] 23.06667

outono_temp_media

## [1] 20.7

inverno_temp_media

## [1] 17.6

Será que em São Paulo chove mais no verão ou no inverno? Escreva um código para verificar se chove mais no verão ou no inverno em São Paulo.

Verifique se a temperatura média no outono é diferente da do inverno.

Qual seria a precipitação em cada mês do ano se chovesse o dobro? Crie uma variável chamada prec2x. Imprima o resultado de prec2x.

Qual a diferença de precipitação entre primavera e verão (nesta ordem)? Chame a nova variável de dif_prec. Imprima o resultado.

2.8 Matrizes

Em R, uma matriz é uma coleção de elementos do mesmo tipo de dados (numeric, character ou logical) arrumados em um número fixo de linhas e colunas. Como está organizada em linhas e colunas, uma matriz é bi-dimensional.

Uma matriz pode ser criada com a função matrix().

Por exemplo se queremos construir uma matriz com 9 elementos e 3 linhas, podemos usar o código a seguir:

#para criar uma matriz com 3 linhas
matrix(1:9, byrow = TRUE, nrow = 3)

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

Nesta função, o primeiro argumento 1:9 é a coleção de elementos que R vai formar em colunas e linhas em uma matriz. Neste caso será 1:9, ou seja c(1, 2, 3, 4, 5, 6, 7, 8, 9).

O segundo argumento byrow indica que a matriz vai ser preenchida pelos números de 1 a 9 seguindo as linhas (by row = por linha). Se queremos preencher segundo as colunas, o argumento deverá ser byrow = FALSE.

O terceiro argumento nrow indica que a matriz deve ter 3 linhas (nrow significa number of rows).

Vamos construir uma matriz para ver como se distribui a população de São Paulo segundo tipo de assentamento. Dividimos os assentamentos em: assentamentos regulares, aglomerados subnormais (definidos pelo IBGE) e assentamentos precários, em três faixas etárias: de 0 a 19 anos; de 20 a 59 anos e + de 60 anos de idade.

Para construir uma matriz, vamos primeiro criar os vetores das populações por faixa etária de cada tipo de assentamento. Chame o primeiro vetor de ‘ass_reg’ e atribua os seguintes valores: 2540608, 5794529, 1253256.

O segundo vetor terá o nome de ‘ass_prec’ e conterá os seguintes valores: 97712, 161663, 19225.

O terceiro vetor será o ‘agsn’, com: 539918, 777051, 65114

#para criar o vetor 'ass_reg'
ass_reg <- c(2540608, 5794529, 1253256)
#para criar o vetor 'ass_prec'
ass_prec <- c(97712, 161663, 19225)
#para criar o vetor 'agsn'
agsn <- c(539918, 777051, 65114)

Agora podemos definir a matriz com 3 linhas, seguindo a sequência das linhas. Vamos chamá-la de pop_sp_matrix.

#para criar a matriz com os 3 vetores 
pop_sp_matrix <- matrix(c(ass_reg, ass_prec, agsn), nrow = 3, byrow = TRUE)
#para imprimi-la
pop_sp_matrix

##         [,1]    [,2]    [,3]
## [1,] 2540608 5794529 1253256
## [2,]   97712  161663   19225
## [3,]  539918  777051   65114

Como você viu, não temos nomes para linhas e colunas. Vamos gerar dois vetores contendo os nomes. Um para as linhas, outro para as colunas. As linhas vão receber o nome de ‘tipos’ e vão conter: ‘ass. regular’, ‘ass. precário’ e ‘agsn’. A ordem de entrada dos elementos precisa ser correta. Lembre-se que por serem texto, precisam estar entre aspas.

#para criar o vetor 'tipos'
tipos <- c("ass. regular", "ass. precário", "agsn")

As colunas serão chamadas de ‘idades’ e deverão conter: 0 a 19, 20 a 59, 60 e mais

#para criar o vetor 'idades'
idades <- c("0 a 19", "20 a 59", "60 e mais")

Para atribuir os nomes das colunas à matriz, vamos usar a função colnames().

#para dar nomes às colunas
colnames(pop_sp_matrix) <- idades

Você consegue atribuir o nome ‘tipos’ para as linhas usando a função rownames()? Imprima novamente a matrix.

#para dar nomes às linhas
rownames(pop_sp_matrix) <- tipos

2.9 Cálculos em Matrizes

Gostaríamos de saber qual a população total em cada tipo de assentamento. Para isso, usamos a função rowSums() para criar ‘total’

#para somar as linhas
tot_rows <- rowSums(pop_sp_matrix)
#Imprima para ver o resultado
tot_rows

##  ass. regular ass. precário          agsn 
##       9588393        278600       1382083

Seria interessante criarmos uma nova coluna com os totais encontrados. Para isso vamos adicionar o vetor ‘total’ à matriz ‘pop_sp_matrix’ e chamar de ‘pop_sp_tot_rows’, usando a função cbind(). A letra ‘c’ neste caso, indica ‘column’

#para unir a coluna 'tot_rows' à matriz
pop_sp_tot_rows <- cbind(pop_sp_matrix, tot_rows)
#imprima pop_sp_total
pop_sp_tot_rows

##                0 a 19 20 a 59 60 e mais tot_rows
## ass. regular  2540608 5794529   1253256  9588393
## ass. precário   97712  161663     19225   278600
## agsn           539918  777051     65114  1382083

Usando o raciocínio percorrido para adicionar uma nova coluna com a função cbind(), você seria capaz de acrescentar uma linha com os totais de cada faixa etária na matriz ‘pop_sp_total’ usando as funções colSums() e rbind()?

#para somar as colunas
tot_cols <- colSums(pop_sp_tot_rows)
#para unir a linha 'tot_cols' à matriz
pop_sp_total <- rbind(pop_sp_tot_rows, tot_cols)
#Imprima para ver o resultado
pop_sp_total

##                0 a 19 20 a 59 60 e mais tot_rows
## ass. regular  2540608 5794529   1253256  9588393
## ass. precário   97712  161663     19225   278600
## agsn           539918  777051     65114  1382083
## tot_cols      3178238 6733243   1337595 11249076

Imagine, hipoteticamente, que 90% da população, independente da faixa etária e tipo de assentamento, tenha tomado todas as doses da vacina contra a COVID-19 em São Paulo. Para saber quantas pessoas ainda precisam tomá-la podemos multiplicar toda a matriz por 0.10. Chame o resultado de ‘pop_sp_10’

#para multiplicar a matriz por 10%
pop_sp_10 <- pop_sp_total * 0.10
#para visualizar o resultado
pop_sp_10

##                 0 a 19  20 a 59 60 e mais  tot_rows
## ass. regular  254060.8 579452.9  125325.6  958839.3
## ass. precário   9771.2  16166.3    1922.5   27860.0
## agsn           53991.8  77705.1    6511.4  138208.3
## tot_cols      317823.8 673324.3  133759.5 1124907.6

Mas na verdade descobrimos que a cobertura vacinal variou entre as faixas etárias e também entre os tipos de assentamentos. Criamos uma matriz com os valores (hipotéticos) de cobertura vacinal.

#vetor da cobertura vacinal
cob_vac <- c(0.59, 0.88, 0.93, 0.8, 0.61, 0.79, 0.75, 0.66, 0.56, 0.65, 0.72, 0.64, 0.59, 0.77, 0.8, 0.7)
#para criar a matriz
cob_vac_matrix <- matrix(cob_vac, nrow = 4, byrow = TRUE)
#para imprimir a matriz
cob_vac_matrix

##      [,1] [,2] [,3] [,4]
## [1,] 0.59 0.88 0.93 0.80
## [2,] 0.61 0.79 0.75 0.66
## [3,] 0.56 0.65 0.72 0.64
## [4,] 0.59 0.77 0.80 0.70

Agora queremos saber quantas pessoas já foram vacinadas por faixa etária e tipo de assentamento. Para isso, multiplique as duas matrizes.

#para multiplicar as matrizes
sp_cob_vac <- pop_sp_total * cob_vac_matrix
#para visualizar o resultado
sp_cob_vac

##                   0 a 19   20 a 59  60 e mais  tot_rows
## ass. regular  1498958.72 5099185.5 1165528.08 7670714.4
## ass. precário   59604.32  127713.8   14418.75  183876.0
## agsn           302354.08  505083.2   46882.08  884533.1
## tot_cols      1875160.42 5184597.1 1070076.00 7874353.2

Veja que a aritmética entre matrizes só é possível quando elas têm o mesmo número de linhas e colunas.

2.10 Seleção em Matrizes

Já vimos que para selecionar um elemento de um vetor podemos usar colchetes [ ]. O mesmo acontece com a seleção em matrizes. A diferença é que um vetor é unidimensional enquanto uma matriz é bidimensional. Desta forma, dentro dos colchetes precisamos indicar qual a linha e qual a coluna correspondente ao elemento que desejamos selecionar.

Outro aspecto que precisamos recordar é que quando desejamos selecionar um intervalo de dados podemos usar : para indicar que os dados estão em uma sequência. Por exemplo, para selecionar elementos que estão nas linhas 23 a 35, na coluna 12: [23:35,12].

Ao selecionar uma linha inteira definimos apenas o número da linha. Por exemplo, seleção da linha 63: nomearquivo[63,]. Se fosse a coluna 31, seria [,31].

Com base na matriz de população por tipo de assentamento e faixa etária, selecione a população de 20 a 59 anos que mora em aglomerados subnormais. Chame a variável de ‘agsn_20a59’. Se achar mais fácil, imprima a matriz ‘pop_sp_total’ para visualizar os dados. Observe que a matriz de dados é 4 x 4 (os nomes das linhas e das colunas não contam).

#para visualizar a matriz
pop_sp_total

##                0 a 19 20 a 59 60 e mais tot_rows
## ass. regular  2540608 5794529   1253256  9588393
## ass. precário   97712  161663     19225   278600
## agsn           539918  777051     65114  1382083
## tot_cols      3178238 6733243   1337595 11249076

#para selecionar o que se deseja e criar uma nova variável
agsn_20a59 <- pop_sp_total[3,2]
#para visualizar o resultado
agsn_20a59

## [1] 777051

Selecione a linha inteira dos assentamentos precários e chame a nova variável de ‘pop_ass_prec’.

#para atribuir 'pop_ass_prec' à seleção da linha inteira
pop_ass_prec <- pop_sp_total[2,]
#para visualizar
pop_ass_prec

##    0 a 19   20 a 59 60 e mais  tot_rows 
##     97712    161663     19225    278600

2.11 Fatores

Fatores armazenam dados de variáveis categóricas (ou qualitativas). Enquanto as variáveis contínuas correspondem a infinitos valores, as variáveis categóricas só podem pertencer a um número limitado de classes.

Um bom exemplo de variável categórica são as classes de raça ou cor (segundo classificação do IBGE). No Censo Demográfico brasileiro há 5 grupos autorreferidos de raça ou cor: preta, branca, amarela, indígena ou parda. Deixando de lado todas as discussões sobre a definição e nomes destas categorias, podemos criar um vetor atribuindo a cada pessoa entrevistada uma cor ou raça referida por ela.

Vamos criar um vetor chamado ‘vetor_cor’ para uma amostragem de 10 pessoas, cujas respostas ordenadas foram: preta, preta, branca, parda, branca, amarela, indigena, preta, branca, parda. Como as respostas são em texto, é necessário usar ““.

vetor_cor <- c("preta", "preta", "branca", "parda", "branca", "amarela", "indigena", "preta", "branca", "parda")

#Imprima para ver o vetor
vetor_cor

##  [1] "preta"    "preta"    "branca"   "parda"    "branca"   "amarela"  "indigena" "preta"   
##  [9] "branca"   "parda"

Para que o R reconheça este vetor como um fator, usamos a função factor(). Crie ‘fator_vetor_cor’ usando a função factor(). Imprima para ver o resultado.

#para criar o fator
fator_vetor_cor <- factor(vetor_cor)
#para visualizar
fator_vetor_cor

##  [1] preta    preta    branca   parda    branca   amarela  indigena preta    branca  
## [10] parda   
## Levels: amarela branca indigena parda preta

Observe que quando imprimimos o objeto do tipo fator, existe a linha “Levels” mostrando todas as categorias encontradas no conjunto de dados.

Os dados categóricos podem ser nominais ou ordinais. Como vimos no fator cor, não existe ordem entre as categorias. Neste caso, eles são listados em ordem alfabética na linha “Levels”.

Uma função muito útil é summary(). Com ela você tem uma boa ideia do conteúdo de cada objeto. Tente summary() para ver ‘vetor_cor’ e em seguida, para ver ‘fator_vetor_cor’.

Qual a diferença entre os dois?

#para ver o resumo do vetor
summary(vetor_cor)

##    Length     Class      Mode 
##        10 character character

#para vero resumo do fator
summary(fator_vetor_cor)

##  amarela   branca indigena    parda    preta 
##        1        3        1        2        3

Em um fator, o ‘summary’ resume o número de elementos presentes em cada categoria. No vetor, ‘summary’ apresenta o comprimento do vetor e o tipo de dados.

Fatores podem ser nominais ou ordinais. Para criar um fator ordinal, é preciso especificar os níveis entre os elementos. Vamos criar um vetor com a vulnerabilidade a inundações de 10 municípios. Chame este vetor de ‘vuln’.

#para criar o vetor
vuln <- c("alta", "baixa", "baixa", "muito alta", "nenhuma", "intermediária", "intermediária", "intermediária", "baixa", "baixa")
#para visualizar
vuln

##  [1] "alta"          "baixa"         "baixa"         "muito alta"    "nenhuma"      
##  [6] "intermediária" "intermediária" "intermediária" "baixa"         "baixa"

Vamos converter o vetor ‘vuln’ em um fator ordenado. Para isso precisaremos indicar a ordem dos níveis. Ordem de elementos segundo vulnerabilidade (nenhuma, baixa, intermediária, alta, muito alta).

#para criar o fator
factor_vuln <- factor(vuln, ordered = T, levels = c("nenhuma", "baixa", "intermediária", "alta", "muito alta"))
#para visualizar o fator criado
factor_vuln

##  [1] alta          baixa         baixa         muito alta    nenhuma       intermediária
##  [7] intermediária intermediária baixa         baixa        
## Levels: nenhuma < baixa < intermediária < alta < muito alta

Em um fator ordenado, as classes aparecem em ordem crescente de acordo com os níveis estabelecidos.

Visualize o summary() de ‘factor_vuln’.

summary(factor_vuln)

##       nenhuma         baixa intermediária          alta    muito alta 
##             1             4             3             1             1

Vamos selecionar e criar novos objetos com os elementos de ‘factor_vuln’. Selecione o elemento 6 e crie um objeto. Selecione o elemento 2 e crie um elemento. Chame de ‘vuln6’ e ‘vuln2’, respectivamente

#para selecionar o elemento 6
vuln6 <- factor_vuln[6]
#para selecionar o elemento 2
vuln2 <- factor_vuln[2]

#para visualizar
vuln6

## [1] intermediária
## Levels: nenhuma < baixa < intermediária < alta < muito alta

vuln2

## [1] baixa
## Levels: nenhuma < baixa < intermediária < alta < muito alta

Agora poderemos comparar ‘vuln6’ com ‘vuln2’. Verifique se ‘vuln6’ é igual a ‘vuln2’.

#para verificar se vuln6 é igual a vuln2
vuln6 == vuln2

## [1] FALSE

Verifique se ‘vuln6’ é maior do que ‘vuln2’.

#para verificar se vuln6 é maior do que vuln2
vuln6 > vuln2

## [1] TRUE

2.12 Referências citadas

AQUINO, J.A. R para cientistas sociais. Ilhéus: Editora da UESC, 2014. 167p.

DATACAMP. 2023. Cornelissen, J. Introduction to R. On-line Course.

DATACAMP. 2023. Robinson, D. Introduction to the Tidyverse. On-line Course.

DATACAMP. 2023. Chapman, J. Data manipulation with Dplyr. On-line Course.